Négation et cut

Cette note de cours a été réalisée d'après le cours de l'ISMRA de Caen, où j'ai repris la partie des notes de cours consacrée à la négation et au Cut. On peut aussi se reporter au diaporama téléchargeable de l'université de Montréal.

L'exécution d'un "programme" Prolog passe toujours par des retours en arrière. On note, par convention, l'exécution de P(X) par:

Le cut

Présentation

Le predicat prédéfini " ! " - le cut - permet d'empêcher le retour en arrière.

Ainsi, alors que la règle p(X) :- a(X), b(X). a la boîte d'exécution:

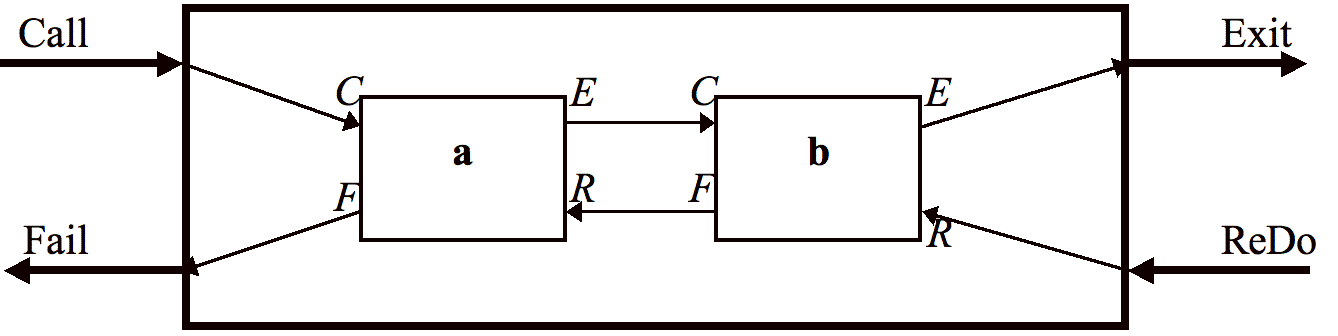
La règle p(X) :- a(X), !, b(X). a la boîte d'exécution suivante :

Une fois un cut franchi :

! coupe toutes les clauses en dessous de lui,
! coupe tous les buts à sa gauche ,
En revanche, possibilité de retour arrière sur les sous buts à la droite du cut.

Les conséquences du cut sont d'améliorer l'efficacité et d'exprimer le déterminisme; mais il revient à faire fonctionner le Prolog comme un langage procédural et il peux introduire des erreurs de programmation vicieuses. Il faut donc l'utiliser avec parcimonie.

Exemple

La fusion de 2 listes triées est déterministe :

On peut donc éliminer les possibilités de retour en arrière :

fusion([], L, L). fusion(L, [], L). fusion([X | XS], [Y | YS], [X | ZS]) :- X < Y, !, fusion(XS, [Y | YS], ZS). fusion([X | XS], [X | YS], [X, X | ZS]) :- !, fusion(XS, YS, ZS). fusion([X | XS], [Y | YS], [Y | ZS]) :- X > Y, !, fusion([X | XS], YS, ZS).

Règles pratiques d'utilisation

Bonne utilisation : cuts verts (ne modifie pas le sens d'un programme). Par exemple, la fusion.

Mauvaise utilisation : cuts rouges (paresseux), par exemple, le minimum

min(X, Y, X) :- X < Y, !. min(X, Y, Y).

Ce prédicat conduit bien au calcul du minimum pour la première solution. Le cut est nécessaire pour éviter de produire une seconde solution au cours d'un retour en arrière. Si on a la règle :

P :- B1 , ..., Bi, min(2, 3, Z), Bj, ..., Bn .

À la première exécution, Z = 2 . Si on revient en arrière à cause d'un échec des buts Bj,..., Bn et si min/3 ne comporte pas de cut, on obtient Z = 3 car min/3 aurait pu produire deux solutions. On repartirait alors avec cette valeur pour prouver buts Bj,..., Bn.

Autre cut rouge:

ifthenelse(P, Q, R):- P, !, Q. ifthenelse(P, Q, R):- R.

La négation

Synopsis

Le symbole de la négation: "\+" (anciennement not )

Un programme logique exprime ce qui est vrai. La négation, c'est donc ce que l'on ne peut pas prouver :

Si G réussit alors \+ G échoue,
Si G échoue alors \+ G réussit.

Définition

Le prédicat not peut être défini par :

not(P) :- P, !, fail. not(P) :- true.

Exemple et précautions

Avec un not, il vaut mieux que les variables soient instanciées :

?- \+ member(X, [a, b]). No.

Le programme identifie X à une des variables, réussit et le not le fait échouer.

De même dans une règle, il faut veiller à l'instanciation des variables. Avec le programme :

marie(francois). etudiant(rene). etudiant_celibataire(X) :- \+ marie(X), etudiant(X).

La requête suivante échoue :

?-etudiant_celibataire(X). No.

car X s'apparie à françois puis le not fait échouer. Alors que :

?- etudiant_celibataire(rene). Yes.

réussit car X = rene donc \+ marie(rene) est vrai.

Pour que la règle produise les résultats attendus, il faut inverser les sous buts :

étudiant_célibataire(X) :- etudiant(X), \+ mari(X).

Ainsi X sera instancié avant d'être soumis au \+ .

Retour au TD.